A simplified way to assess the Heat Release Rate

The Heat Release Rate (HRR) is a fundamental parameter to describe the fire hazard. A simplified method to estimate HRR is analyzed in order to rapidly assess a fire hazard in FDS. Generally, in fire engineering, a the traditional fire development curve approximate the behavior of the HRR.

The Heat Release Rate (HRR) is the rate expressed in MW at which the combustion produces heat and the thermal power is released [1]. Its equations govern the amount of heat released within time and it assess the design fire size.

Only appropriate test are able to measure the actual heat release rate produced by the combustion of an item. In FDS the HRR can be simplified by means of the conventional fire development curve, which consider an overestimation of approximately 20% respect to the effective HRR [2].

Here it is exposed a simplified method to estimate the heat release rate and its traditional fire development curve, as indicated by the Italian Fire Code [3] and the Eurocode 1991-1-2 Appendix E [4].

The Heat Release Rate Conventional Curve

Generally, four stages describes the conventional Heat Release Rate curve: incipient, growth, stationary phase and decay. Flashover is a rapid increase in fire growth and consequently sudden transition to a fully developed fire. The times in which the fire development stages follow one another are:

• the time of initial growth (t₀)
• the time in which the HRR is reaches its peak (t_max)
• time of initial decay (t_decay)
• the time to decay burnout (t_tot).

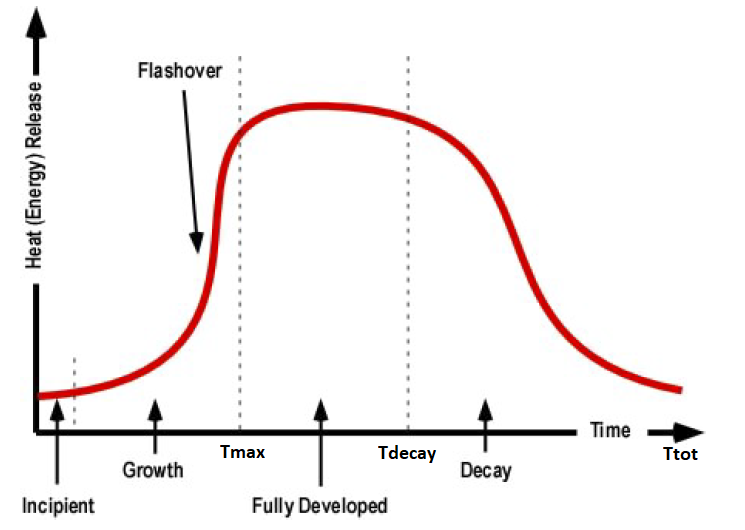
A real fire don’t always follow the behavior described by the conventional fire development curve. In reality, the fire growth speed, peak heat release rate, and duration of burning depends on the type of fuel and the ventilation availability.

The following expressions are able to describe the typical stages of the fire development for fires where no suppression takes place.

Growth Stage

The following expression describes the growing phase:

HRR_(t)= 1000 (t/t_α)² for t<t_max

where:

• HRR_(t) is the heat release from the fire hazard
• t is time
• t_α is the time needed to reach the heat release of 1000 KW

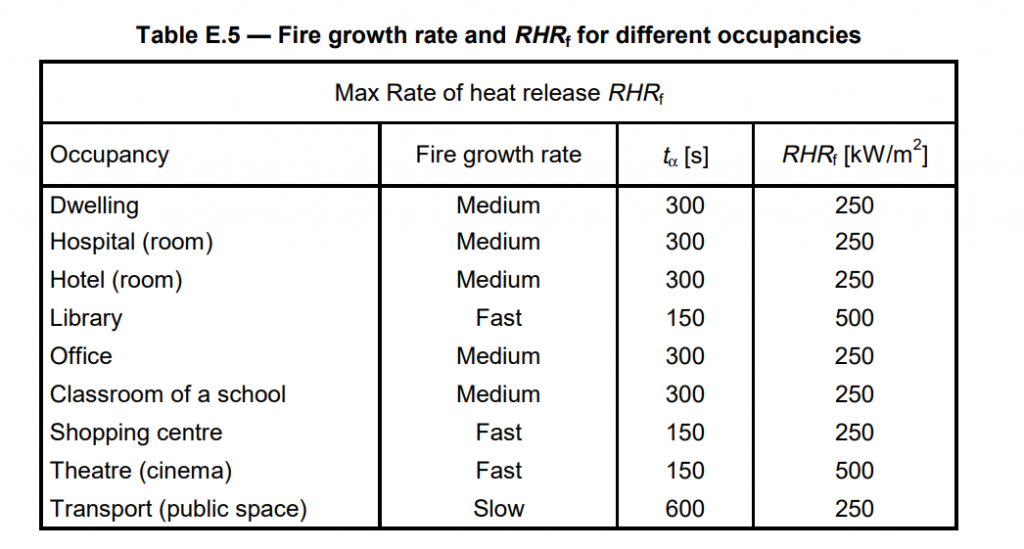
For instance, the Eurocode 1 UNI EN 1991-1-2 Appendix E define some values of t_α for different occupancies, as shown by the following table E.5 [4]. Ultra-fast fires the value of t_α is 75 seconds. For occupancies not included in the Appendix E or literature, the evaluation of t_α depends on the expertise of the developer.

Stationary Phase

In the stationary phase of the fire hazard the HRR is steady and remains constant at its peak value till the decay phase starts.

HRR_(t) = HRR_max for t_max<t<t_decay

The HRR maximum value depends on what governs the fire development. Fuel o ventilation can control the fire growth of a fire hazard.

Known the value of HRR_max, determine the time in which the stationary phase of the fire (t_max) starts as follow:

t_max = √(HRR_max ⋅ t_α² / 1000)

Fuel Controlled Fire

The fuel controlled fire depends on the amount of fuel available and the lack of oxygen limits its growth. Therefore, the fire growth only depends on the fire load area:

HRR_max=HRR_f ⋅ A_f

Where:

• HRR_f is the thermal heat energy release per unite of gross floor area. Appendix E.4 of Eurocode 1 UNI EN 1991-1-2 shows some values of HHR_f for different occupancies [kW/sqm];
• A_f is the gross floor area of the compartment in case of uniform distribution of the fire load, or the floor area effectively occupied by the fire load [sqm].

Ventilation controlled fire

The ventilation controlled fire depends on the comburent availability, which can come through the ventilation openings and limits the fire growth. The following expression determine the HRR_max, for a ventilation controlled fire:

HRR_max = 0,10 ⋅ m ⋅ H_u ⋅ A_v ⋅ √h_eq

Where:

• m is the combustion factor. The Italian fire code gives a value of m of 0,8 for wood and 1 for other combustible materials
• H_u is the calorific value of wood, equal to 17,5 MJ/kg
• A_v is the opening area [sqm]
• h_eq is the equivalent height of the openings [m]

Decay

The fire’s stationary state ends at t_decay, time in which the decay starts and 70% of the initial thermal energy (q_f x A_f) is released, where qf is the fire load.

If the initial thermal energy is sufficient to overcome the propagation phase and reach the heat rate release maximum value:

70% ⋅ q_f ⋅ A_f ≥ 1/3 ⋅ 1000/ t_α² ⋅ t_max³

Therefore, calculate the time in which the stationary phase finish and the decay stars, as follow:

t_decay = t_max + ( 70% ⋅ q_f ⋅ A_f ≥ 1/3 ⋅ 1000/ t_α² ⋅ t_max³) / HRR_max

If the initial thermic energy is not sufficient to overcome the propagation phase, than the HRR curve will reach the peak and then directly starts to decay.

Consequently, The decay phase start at t_decay and will finish at t_tot when the thermal energy released is null.

T_tot is calculated taking in consideration that the remaining 30% of the initially available thermal energy is consumed:

t_tot = t_decay + (2 ⋅ 30% ⋅ q_f ⋅ A_f / HRR_max)

The following equation describes the HRR curve trend of the decay phase:

HRR_(t) = HRR_max ⋅ (t_tot – t) / (t_tot – t_decay) for t_decay ≤ t ≤ t_tot

For more information about the Cloud HPC and FDS, check the cloud hpc blog.

Bibliography

[1] Morgan J. Hurley, Editor-in-Chief, “SFPE Handbook of Fire Protection Engineering” 2015

[2] Andrea Dusso, Stefano Grimaza, Ernesto Salzanob, “Rapid Estimation of the Heat Release Rate of Combustible Items”, 2016

[3] D.M. 03/08/2015 and D.M. 14/04/2019, Italian Fire Code

[4] BS EN 1991-1-2:2002, “Eurocode 1:Actions on structures Part 1-2”, 2002

[5] Battalion Chief Ed Hartin, MS, EFO, MIFireE, CFO “Fire Development and Fire Behavior Indicators”

---

CloudHPC is a HPC provider to run engineering simulations on the cloud. CloudHPC provides from 1 to 224 vCPUs for each process in several configuration of HPC infrastructure - both multi-thread and multi-core. Current software ranges includes several CAE, CFD, FEA, FEM software among which OpenFOAM, FDS, Blender and several others.

New users benefit of a FREE trial of 300 vCPU/Hours to be used on the platform in order to test the platform, all each features and verify if it is suitable for their needs

---

Contact Name/Surname *

Company Name *

Company address *

City *

State/Province *

Country *CountryAfghanistanAlbaniaAlgeriaAmericaAndorraAngolaAntiguaArgentinaArmeniaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBhutanBissauBoliviaBosniaBotswanaBrazilBritishBruneiBulgariaBurkinaBurmaBurundiCambodiaCameroonCanadaCape VerdeCentral African RepublicChadChileChinaColombiaComorosCongoCosta RicaCroatiaCubaCyprusCzechDenmarkDjiboutiDominicaEast TimorEcuadorEgyptEl SalvadorEmirateEnglandEritreaEstoniaEthiopiaFijiFinlandFranceGabonGambiaGeorgiaGermanyGhanaGreat BritainGreeceGrenadaGrenadinesGuatemalaGuineaGuyanaHaitiHerzegovinaHollandHondurasHungaryIcelandIndiaIndonesiaIranIraqIrelandIsraelItalyIvory CoastJamaicaJapanJordanKazakhstanKenyaKiribatiKoreaKosovoKuwaitKyrgyzstanLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshallMauritaniaMauritiusMexicoMicronesiaMoldovaMonacoMongoliaMontenegroMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNew ZealandNicaraguaNigerNigeriaNorwayOmanPakistanPalauPanamaPapuaParaguayPeruPhilippinesPolandPortugalQatarRomaniaRussiaRwandaSamoaSan MarinoSao TomeSaudi ArabiaScotlandScottishSenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomonSomaliaSouth AfricaSouth SudanSpainSri LankaSt KittsSt LuciaSudanSurinameSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTobagoTogoTongaTrinidadTunisiaTurkeyTurkmenistanTuvaluUgandaUkraineUnited KingdomUnited StatesUruguayUSAUzbekistanVanuatuVaticanVenezuelaVietnamWalesWelshYemenZambiaZimbabwe

Email *

Email

Confirm Email

Privacy *

• I accept the privacy conditions

Privacy Policy

Phone

Send registration